Online Clustering
\[D=\{X^1,X^2,...,X^N\}\] \[X\in R^d\\] \[Cost=(Nd)\]
What if we only care about clusters.
\[C=\{b^1,b^2,...,b^M\}\] \[M<<N\] \[Cost=(Md+N)\]- Which cluster dose a point belong? Win Function
We define the \(X^i\) belongs to the nearest cluster.
\[win(i)=j,\quad s.t.\,min\{|X^i-b^j|\}\]- Now, assume that we already know \(M\)
So first we choose MM random \(b\) from data points, then we iterate all data point, trying to minimize this Error function.
\[E=\frac{1}{N}\sum_{i=1}^{N}||X^i-b^{win(i)}||^2\]We can use gradient descend.
\[E=\frac{1}{N}\sum_{i=1}^{N}||X^i-b^{win(i)}||^2\] \[b^{win(i)}(t+1)=b^{win(i)}(t)-\alpha\nabla E\] \[b^{win(i)}(t+1)=b^{win(i)}(t)+\alpha(X^i-b^{win(i)})\]- Adjustment of \(\alpha(t)\)
- Situation that we do not know \(M\)
Just choose \(M\) from 1 to \(N\), find the kneel point where \(E(M)\) does not decrease sharply.
- Modifying Clustering to fit non-linear situation
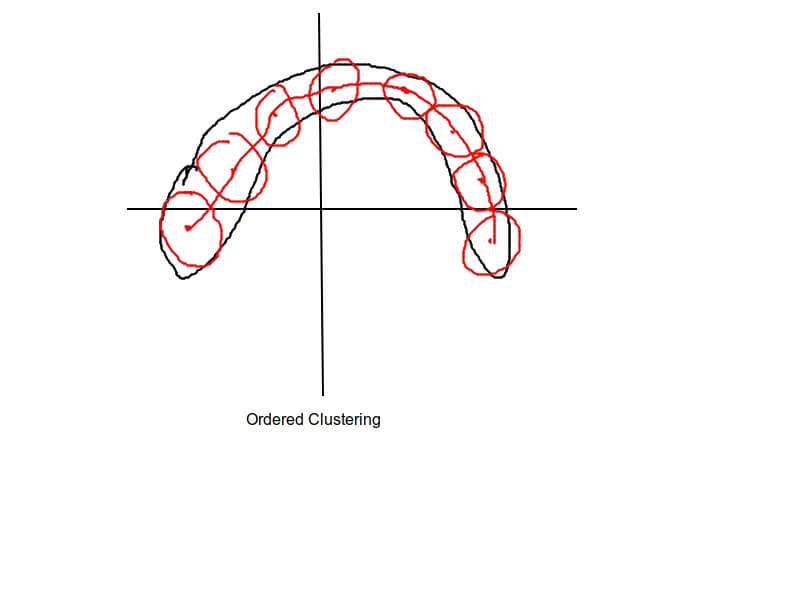
In such case, we can use \(M\) red cluster to this type of data, then connect those cluster center.
We just need to modify the cluster function in order to make sure it cluster in order. \(b^1,b^2,b^3...b^M\)
- Neighbor Factor
We add a neighbor factor to achieve our goal, instead of update a single weight, we update all weight simutaouensly to ensure the order. \(h(c,j)=e^{\frac{-(j-c)^2}{\sigma^2}}\)
In this gaussian distribution, sigma represent how much neighbor will be infected in one iteration, so this will decrease as iteration times increase, basically it follows the same exponatial decrease formula like the \(learning\space rate\) does.
So we now have:
\[b^{j}(t+1)=b^{j}(t)+h(win(i),j)\alpha(X^i-b^{j})(learning\space rate=\alpha)\]- 2-D case
In the above, we only consider when the \(b_i\) lies in a one dimensional line, but we can have other high dimensional space like a plane, so we can let \(b_i\) lies in a 2-D net or a 3-D cube to achieve our goal. \(b^{i}\rightarrow b^{i,j}\)
作者:卢弘毅
